Значение двоичного кода – почему компьютеры работают с единицами и нулями. В какой системе счисления работает компьютер. | Новости, гайды, обзоры, рецензии все о лучших компьютерных играх

Содержание

Она имеет основание 16. В системе используются цифры 0-9 и буквы A-F для выражения чисел. Буквы: 10, 11, 12, 13, 14 и 15 соответственно.

Основы систем счисления

Когда я занялся кодированием, я понял, что недостаточно хорошо разбираюсь в системах нумерации. Однако я использовал 2, 8, 10, 16 систем и переводил их друг в друга, но все происходило автоматически. Прочитав множество публикаций, я был удивлен, что нет статьи простым языком на такую базовую тему. Поэтому я решил написать свою статью, в которой постараюсь описать основные системы счисления в понятной и упорядоченной форме.

Система счисления — это способ обозначения (представления) чисел.

Что это значит? Например, вы видите перед собой ряд деревьев. Ваша задача — сосчитать их. Для этого можно загибать пальцы, делать насечки на камне (одно дерево — один палец или одна насечка) или назначить 10 деревьев одному предмету, например, камню, а одно дерево — палке, и положить их на пол, пока вы считаете. В первом случае число предстает в виде серии изогнутых пальцев или зарубок, во втором — в виде композиции из камней и дерева, причем камни находятся слева, а дерево — справа.

Системы нумерации делятся на позиционные и непозиционные, позиционные системы, в свою очередь, на однородные и смешанные. Непозиционная нумерация является самой старой; в ней каждая цифра числа имеет значение, которое не зависит от ее позиции (разряда). То есть, если у вас 5 строк — то и число будет 5, потому что каждая строка, независимо от ее положения в строке, соответствует одному элементу.

Позиционная система — значение каждого разряда зависит от его положения (позиции разряда) в числе. Например, число 10 является символом позиции. Возьмем число 453. Число 4 представляет собой число сотен и соответствует числу 400, число 5 представляет собой число десятков и соответствует числу 50, а число 3 представляет собой число единиц и соответствует числу 3. Как видите, чем больше цифр, тем выше значение. Общее число можно представить как сумму 400+50+3=453.

Однородная система — для всех цифр (разрядов) числа общее количество допустимых знаков (цифр) одинаково. Возьмем для примера упомянутую выше систему 10. Если вы записываете число в однородной системе 10, вы можете использовать только одну цифру от 0 до 9 в каждом разряде. Так, 450 разрешено (1-я цифра — 0, 2-я — 5, 3-я — 4), а 4F5 — нет, потому что символ F не входит в набор цифр от 0 до 9.

Смешанная система — в каждом разряде (позиции) числа набор допустимых символов (цифр) может отличаться от наборов других разрядов. Типичным примером является система измерения времени. Цифры секунд и минут могут иметь 60 различных цифр (от «00» до «59»), цифры часов могут иметь 24 различные цифры (от «00» до «23»), цифры дней могут иметь 365 цифр и так далее.

Непозиционные системы

С того момента, как мы научились считать, мы должны были писать цифры. Сначала все было очень просто: насечка или линия на поверхности соответствовала объекту, например, фрукту. Так родилась первая система нумерации — система единиц.

Система нумерации единиц измерения

Число в этой системе нумерации состоит из тире (штриха), которое соответствует значению числа. Таким образом, урожай из 100 фиников будет соответствовать числу, состоящему из 100 столбиков. Однако эта система имеет очевидные недостатки — чем больше число, тем длиннее ряд полос. Более того, легко ошибиться, случайно добавив лишнюю полосу или, наоборот, опустив полосу.

Для простоты люди стали группировать палочки по 3, 5 или 10 штук. Таким образом, каждая группа соответствовала определенной точке или объекту. Первоначально для счета использовались пальцы, поэтому появились первые обозначения для групп из 5 и 10 штук (единиц). Это привело к появлению более удобных систем записи чисел.

Древнеегипетская десятичная система

В Древнем Египте для обозначения чисел 1, 10, 10 2, 10 3, 10 4, 10 5, 10 6, 10 7 использовались специальные символы (нумералы). Вот некоторые из них:

Почему они называются десятичными числами? Как описано выше, люди начали группировать символы вместе. В Египте они решили сгруппировать по 10 и оставить число «1» неизменным. В этом случае число 10 называется основанием десятичной системы, а каждый символ в той или иной степени является представлением числа 10.

В древнеегипетской системе счисления числа записывались в виде комбинации этих символов, каждый из которых повторялся максимум девять раз. Итоговое значение было равно сумме элементов числа. Следует отметить, что этот способ определения величины входит в каждую неположительную систему счисления. Примером может служить число 345:

Вавилонская шестнадцатеричная система

В отличие от египетских, вавилонские используют только 2 цифры, четный клин для единиц и горизонтальный клин для десятков. Чтобы определить значение числа, нужно разделить изображение числа на цифры справа налево. Новый разряд начинается с появлением прямого клина после обратного клина. Возьмем для примера число 32: число 60 и все его силы обозначаются как «1» таким же образом с помощью прямого клина. По этой причине вавилонскую систему счисления также называют шестнадцатеричной. Вавилоняне записывали все числа от 1 до 59 в неположительной десятичной системе, а большие числа — в положительной системе, основанной на 60. Номер 92: Номер не был уникальным, потому что не было номера для нуля. Представление числа 92 может означать не только 92 = 60+32, но и, например, 3632 = 3600+32. Для определения абсолютного значения числа был введен специальный символ, обозначающий опущенную шестнадцатеричную цифру, соответствующую появлению цифры 0 в десятичном наборе чисел: число 3632 теперь следует записывать следующим образом:

Вавилонская шестнадцатеричная система была первой системой счисления, частично основанной на позиционном принципе. Эта система нумерации используется и сегодня, например, для определения времени — час состоит из 60 минут, а минута из 60 секунд.

Позиционные системы счисления

Как уже упоминалось, первые предпосылки для возникновения позиционной системы идут из древнего Вавилона. В Индии эта система приняла форму десятичного числа с применением нуля, и арабы заимствовали эту систему счисления у индийцев, от которых ее переняли европейцы. По какой-то причине европейцы приняли ее как арабскую систему счисления.

Десятичная система счисления

Это одна из наиболее часто используемых систем счисления. Мы используем его, когда называем цену товара или номер автобуса. Каждая цифра в позиции может содержать только одно число от 0 до 9. Основой системы является число 10.

Например, возьмем число 503. Если бы это число было записано в неположительной системе, то его значение было бы 5+0+3 = 8. Но поскольку у нас позиционная система счисления, каждая цифра числа должна быть умножена на основание системы mul, в данном случае число «10», возведенное в степень, равную количеству цифр. Таким образом, значение равно 5*10 2 + 0*10 1 + 3*10 0 = 500+0+3 = 503. Чтобы избежать путаницы при работе сразу с несколькими системами счисления, основание указывается как нижний индекс. Следовательно, 503 = 503.₁₀.

Помимо десятичной системы счисления, особого внимания заслуживают системы 2, 8 и 16.

Двоичная нотация

Эта система в основном используется в компьютерных технологиях. Почему это была не 10 система, к которой мы привыкли? Первая счетная машина была разработана Блезом Паскалем, который использовал в ней десятичную систему, что оказалось непрактичным в современных электронных машинах, так как необходимо было производить устройства, способные работать в 10 шагах, что увеличивало их цену и размер машины. Эти недостатки устраняются элементами, используемыми во 2-й системе. Однако эта система была разработана задолго до изобретения компьютера и имеет свои «корни» в культуре инков, где использовалась кипу — сложные веревочные сетки и узлы.

Двоичная позиционная нумерация основана на 2 и использует 2 знака (цифры) для записи числа: 0 и 1. В каждом разряде допускается только одна цифра, либо 0, либо 1.

Примером может служить число 101. Это соответствует числу 5 в десятичной системе счисления. Каждая цифра двоичного числа должна быть умножена на основание «2», которое возводится в степень, равную номеру цифры для преобразования из 2 в 10. Таким образом, число 101₂ = 1*2 2 + 0*2 1 + 1*2 0 = 4+0+1 = 5₁₀.

Хорошо, 2-я система счисления более практична для машин, но мы часто видим и используем числа в 10 на компьютере. Как машина определяет число, которое вводит пользователь? Как числа переводятся из одной системы в другую, если они имеют только два знака — 0 и 1?

Компьютер может работать с двоичными числами (кодами), и их нужно где-то хранить. Для хранения каждой цифры используется скремблер — электронная схема. Он может принимать 2 состояния, одно из которых соответствует нулю, а другое — единице. Для хранения одной цифры используется регистр — набор исполнительных механизмов, количество которых соответствует количеству цифр двоичного числа. Набор регистров является функциональной памятью. Число, содержащееся в регистре, является машинным словом. Арифметические и логические операции со словами выполняются арифметико-логическим блоком (ALU). Регистры пронумерованы для облегчения доступа к ним. Это число называется адресом регистра. Например, если нужно сложить 2 числа, достаточно сослаться на номера ячеек (регистров), в которых они находятся, а не на сами числа. Адреса записываются в 8- и 16-битных системах (см. ниже), поскольку переход от этих систем к двоичной системе и обратно довольно прост. Для преобразования из 2 в 8 число нужно разделить на группы по 3 цифры справа налево, а для преобразования в 16 число нужно разделить на группы по 4. Если в самой левой группе цифр есть недостающие цифры, они заполняются нулями слева, которые называются ведущими цифрами. Например, возьмем число 101100₂. В восьмеричном исчислении это 101 100 = 54₈а в шестнадцатеричной системе это 0010 1100 = 2C₁₆. Все это хорошо, но почему мы видим на экране десятичные цифры и буквы? При нажатии клавиши в компьютер передается определенная последовательность электрических импульсов, и каждому символу соответствует своя последовательность электрических импульсов (нулей и единиц). Программное обеспечение драйвера клавиатуры и дисплея обращается к таблице кодировки символов (например, Unicode, которая может кодировать 65536 символов), определяет, какой символ представлен полученным кодом, и выводит его на экран. Таким образом, тексты и числа хранятся в двоичном коде в памяти компьютера и преобразуются программным обеспечением в изображения на экране.

Для восьмеричной системы мы используем восемь основных знаков, которые заимствованы из десятичной системы. Двоичные триплеты могут принимать значения в диапазоне 0-70 — 7.

Подсчет в двоичном формате

В двоичной системе первая цифра равна 1 в десятичной системе. Вторая цифра равна 2, третья — 4, четвертая — 8 и так далее — каждый раз удваивается. Если вы сложите все эти значения, то получите число в десятичной форме.

1111 (двоичный) = 8 + 4 + 2 + 1 = 15 (десятичный)

Включая 0, существует 16 возможных значений для четырех двоичных цифр. Прокрутите на 8 бит и получите 256 возможных значений. Это требует гораздо больше места для представления, так как четыре цифры в десятичной форме дают 10 000 возможных значений. Конечно, двоичный код занимает больше места, но компьютеры понимают двоичный код гораздо лучше, чем десятичную систему. А для некоторых вещей, например, для логической обработки, двоичная система лучше десятичной.

Следует отметить, что существует еще одна базовая система, используемая в программировании: Шестнадцатеричная. Хотя компьютеры не используют шестнадцатеричную систему, программисты используют ее для представления двоичных адресов в удобочитаемом формате при написании кода. Это связано с тем, что две цифры шестнадцатеричного числа могут представлять целый байт, т.е. они заменяют восемь цифр в двоичной форме. В шестнадцатеричной системе используются цифры 0-9 и буквы от A до F, чтобы получить еще шесть цифр.

Почему компьютеры используют двоичные файлы

Короткий ответ: аппаратное обеспечение и законы физики. Каждый символ на вашем компьютере — это электрический сигнал, и на заре развития вычислительной техники измерение электрических сигналов было гораздо сложнее. Логичнее было бы различать только состояние «включено», представленное отрицательным зарядом, и состояние «выключено», представленное положительным зарядом.

Для тех, кто не знает, почему «off» представлен положительным зарядом: Потому что электроны имеют отрицательный заряд, а больше электронов означает больше тока с отрицательным зарядом.

Итак, первые компьютеры размером с комнату использовали двоичные программы для построения своих систем, и хотя они использовали более старое и громоздкое оборудование, они работали на тех же основных принципах. В современных компьютерах для выполнения двоичных вычислений используется так называемый транзистор.

Ниже приведена схема типичного транзистора:

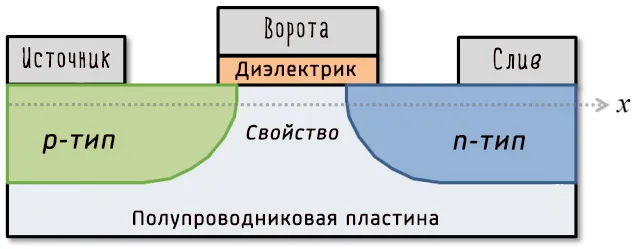
По сути, он позволяет току течь от истока к стоку, когда ток течет в затворе. Это двоичный ключ. Производители могут делать эти транзисторы невероятно маленькими — до 5 нанометров, или размера двух нитей ДНК. Именно так работают современные процессоры, и даже у них могут возникнуть проблемы с различением включенного и выключенного состояния (хотя это связано с нереальным размером их молекул, которые подвержены капризам квантовой механики).

Почему только двоичная система

Теперь вы можете подумать: «Почему только 0 и 1? Почему бы не добавить еще одну цифру?». Хотя это отчасти объясняется традициями компьютерного дизайна, добавление еще одной цифры означает присвоение другого текущего состояния, а не только «выключено» или «включено».

Проблема в том, что если вы хотите использовать несколько уровней напряжения, вам нужен способ легко выполнять вычисления с ними, а современное оборудование, способное делать это, не является полезной заменой двоичным вычислениям. Например, существует так называемый троичный компьютер, который был разработан в 1950-х годах, но с тех пор его развитие застопорилось. Двоичная логика более эффективна, чем двоичная, но эффективной замены двоичному транзистору все еще нет, или, по крайней мере, нет транзистора такого же маленького, как двоичный.

Причина, по которой мы не можем использовать двоичную логику, заключается в способе подключения транзисторов к компьютеру и их использовании для математических расчетов. Транзистор получает информацию на два входа, выполняет функцию и возвращает результат на выход.

Поэтому двоичная математика проще для компьютера, чем любая другая. Двоичная логика может быть легко преобразована в двоичные системы, где true и false соответствуют состояниям on и off.

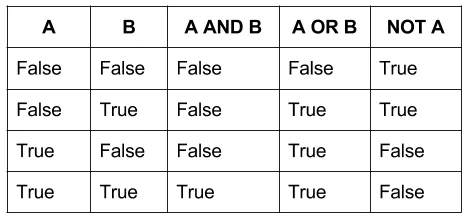
Таблица истинности, выполненная с помощью двоичной логики, имеет четыре возможных выхода для каждой базовой функции. Но поскольку тройные ворота используют три входа, тройная таблица истинности имеет 9 или более входов. В то время как двоичная система имеет 16 возможных операторов (2^2^2), тройная система будет иметь 19683 (3^3^3). Масштабирование становится проблемой, поскольку тривиальные решения, хотя и более эффективны, также экспоненциально более сложны.

Кто знает? В будущем мы можем увидеть тривиальные компьютеры, поскольку двоичная логика борется с проблемами масштабирования. Пока что мир будет продолжать функционировать в двоичном режиме.

Сегодня мы познакомим вас с системами счисления, которые необходимы специалисту по информатике. Мы подробно рассмотрим двоичную и шестнадцатеричную системы счисления.

Десятичная СС

Самые распространенные. Это часть позиционной системы нумерации. Он используется повсеместно в повседневной жизни. Каждый разряд — это одна цифра. Диапазон от 0 до 1 включительно. Основание системы счисления — 10.

Чтобы лучше понять принцип использования, стоит рассмотреть пример — 503. В системе без позиций это выглядело бы так: 5 + 0 + 3 = 8. Вместо этого каждая цифра числа умножается на основание, которое умножается на число, равное номеру цифры.

Чтобы избежать путаницы, символическая нотация может выглядеть следующим образом: 503=503₁₀. Используется более низкий индекс.

Двоичная

Двоичная система счисления используется в основном в устройствах и компьютерах. Это решение было принято потому, что 10-й эсэсовец был слишком дорогим. Это повлияло на стоимость компьютеров.

Необходимо было создать «сокращенную» версию. Основание здесь равно 2. Символы используются для письма:

Каждая цифра имеет только одно соответствующее значение. Пример 101. Это десятичная дробь 5. Чтобы выполнить преобразование из двоичного числа СС в 10, умножьте разряд второго числа на 2. Возведите «2» в степень, равную разряду. Итак, 101₂ будет:

Для работы с кодами компьютер хранит триггер для каждой цифры. Это электронная схема, которая принимает два состояния. Один соответствует «нулю», а другой — «единице».

Для хранения одного числа используется регистр — группа исполнительных механизмов, количество которых соответствует количеству цифр двоичного числа. Число, содержащееся в регистре, называется машинным словом. Чтобы получить к ним доступ, они должны быть пронумерованы. Число — это адрес ячейки.

Шестнадцатеричная система

Шестнадцатеричное представление является очень распространенным форматом в современных компьютерах. Он может использоваться, например, для обозначения цвета.

Она имеет основание 16. В системе используются цифры 0-9 и буквы A-F для выражения чисел. Буквы: 10, 11, 12, 13, 14 и 15 соответственно.

Чтобы лучше понять «принцип работы» этой СС, стоит рассмотреть наглядный пример — 4F15₁₆. Для преобразования в 8 требуется следующее:

Переведите число в двоичную систему.
Разделите его на группы из 3 цифр (элементов).

Для преобразования в 2 каждая цифра представляется как 4-значное число:

Цифры отсутствуют в первой и последней группах. Последняя и последняя цифры заполняются нулями: 0100 1111 0101. Это значение делится на группы по 3 цифры справа налево. Результат: 010 011 110 101.

Чтобы увидеть результат, каждая двоичная группа должна быть переведена в восьмеричную систему. Цифры умножаются на 2 n, где n — номер той или иной цифры. На выходе получается 2368₈.

Восьмеричная и шестнадцатеричная системы счисления широко изучаются в школьных компьютерных курсах. Они не очень полезны для обычных пользователей, но они полезны для тех, кто хочет углубиться в программирование.

Сегодня мы познакомим вас с системами счисления, которые необходимы специалисту по информатике. Мы подробно рассмотрим двоичную и шестнадцатеричную системы счисления.

Шестнадцатеричная система

Это отличается от привычного двоичного и десятичного количества цифр. В нем используется последовательность цифр от 0 до 15, причем в качестве цифр выступают от десяти до пятнадцати латинских букв.

Иллюстрация Шестнадцатеричная система счисления

Этот формат используется в программировании для простой записи байта информации, а также в веб-дизайне, например, для кодирования цветовой палитры. Вместо длинной восьмиразрядной двоичной нотации используются только два бита. Максимальное двузначное значение в этой системе можно представить как FF, т.е. 1111 1111 в двоичной системе или 255 в десятичной.

Рисунок Различия между системами расчета

Иногда перед значением встречается префикс 0x, указывающий на то, что следующее число следует интерпретировать как шестнадцатеричное: 0x8E — число 142 в десятичной системе счисления.

0x868 — 0x868 — префикс на картинке

Так все-таки зачем такие сложности?

Конечно, для всех будет лучше, если в разных районах будет использоваться одна система нумерации. К сожалению, в цифровом мире дело обстоит иначе: известная десятичная система проста, но компьютерное оборудование ее не понимает, а двоичную систему невозможно прочитать. Шестнадцатеричная система делает код несколько более читабельным, но только для просвещенных, которые могут использовать HEX-процессоры.

Таким образом, hex является своего рода переходным состоянием между машинным и человекочитаемым кодом.

Фотодекодированный двоичный код

Позиционная система счисления — это система счисления, в которой числовой эквивалент («вес») цифры зависит от ее положения в системе счисления.

Вычитание. Отрицательная форма числа. Дополнительный код.

Дополнительный код номера

В таблице приведены двоичные коды для положительных и отрицательных чисел. Такой способ записи чисел называется комплементарным кодом и позволяет использовать один и тот же сумматор для вычисления разности. Как и сумма, разность вычисляется побитно путем передачи бита переноса по цепочке.

Вычитание чисел в сумматоре

Бит переноса старшего разряда сохраняется для последующего использования и, как мы увидим позже, играет довольно важную роль.

В форме видео.

Поддержите эту статью, перепечатав ее, если она вам понравилась, и подпишитесь, чтобы ничего не пропустить. Также посетите канал YouTube для получения интересных материалов в видеоформате.

Набор правил для записи чисел на символьных цифровых конечных множествах. Одна и та же последовательность может быть представлена разными числами в разных «системах письма». Примером может служить 11 в десятичной системе счисления, три в двоичной и два в троичной.

Что такое система счисления в информатике?

Люди считают уже давно. Для этого мы используем системы, которые связывают уникальные символы с определенными значениями. Это называется системой счисления и является методом, который мы используем для представления и управления числами.

Система чисел должна иметь уникальные символы для каждого значения, быть последовательной, обеспечивать сопоставимые значения и быть легко воспроизводимой.

Вы, вероятно, знакомы с десятичной системой, которая является основой человеческого способа счета. Десятичная система основана на числе 10, поскольку она предусматривает 10 знаков для представления всех чисел:

Мы, люди, используем десятичную систему, потому что у нас есть 10 пальцев, на которых мы можем основывать наши числа, но у машин нет такой роскоши. Поэтому мы создали другие системы счисления, которые выполняют ту же функцию. Компьютеры представляют информацию иначе, чем люди, поэтому нам нужны разные системы для представления чисел.

Компьютеры поддерживают следующие системы счисления:

Бинарные
Октава
Десятичная:
Десятичные числа основаны на следующих таблицах.

Введение в двоичную систему счисления

Компьютер использует биты для представления информации. Бит — это самая основная единица хранения данных в компьютере. Важной частью компьютеров является транзистор. Подобно выключателю света, транзистор либо пропускает ток, либо не пропускает его. Поэтому существует только два состояния: включено и выключено.

Каждое число в компьютере — это электрический сигнал. На заре развития компьютеров электрические сигналы имели состояние «включено» (отрицательный заряд) и состояние «выключено» (положительный заряд). Это своего рода бинарный переключатель.

Эти два состояния могут быть представлены одним из двух символов: 1 и 0. Это означает, что основой двоичной системы счисления является 2. Для представления каждого числа необходимы только символы.

Базовые числа для двоичной системы просты: 0 — низкое состояние, 1 — высокое состояние.

Вместо того чтобы представлять числа в виде отдельных единиц (например, число 10 или 400), мы используем группы единиц и нулей. Например, вот как это выглядит, когда компьютер считает до 10:

Это называется двоичной системой счисления. Каждая двоичная цифра называется битом. Когда дело доходит до размещения значений и цифр в этой системе, мы размещаем значения, соответствующие возрастающей силе 2 слева направо.

Крайний правый разряд называется младшим значащим битом (LSB), а крайний левый разряд — старшим значащим битом (MSB).

Для изменения значения числа на уровне машинного кода можно манипулировать левым и правым битами с помощью побитовых операторов.

Преобразование между десятичным и двоичным числами

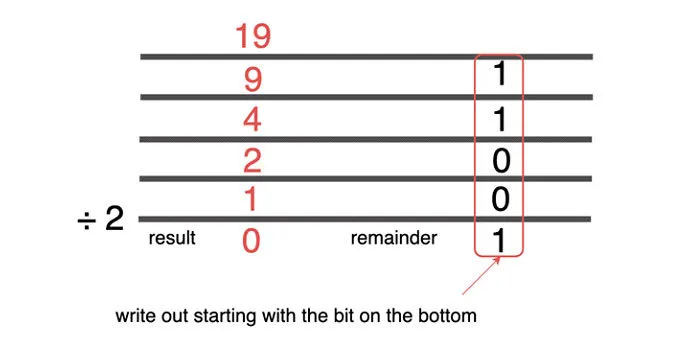
Теперь, когда мы знаем основы двоичной системы, давайте узнаем, как преобразовать десятичные числа в двоичные. Начнем с преобразования двоичного числа в десятичное.

Мы знаем, что двоичная система имеет значения места степени 2. Эти значения являются весами для цифр (0 или 1) в этих позициях. И вот как это работает:

Мы умножаем каждую цифру на ее вес (ее положение умножается на 2) Мы складываем их вместе, чтобы получить десятичное число

Итак, давайте возьмем двоичное число 11111010 и переведем его в десятичную систему счисления.

Введение в шестнадцатеричную систему счисления

Теперь, когда мы немного узнали о двоичной системе, давайте рассмотрим другую систему, широко используемую в компьютерах: шестнадцатеричную.

Двоичные числа легко понять компьютерам, но не так просто людям. А при работе с большими числами трудно писать без ошибок. Чтобы решить эту проблему, мы можем разделить двоичные числа на группы по четыре бита, чтобы сформировать шестнадцатеричную систему счисления.

Шестнадцатеричная система является более компактным способом представления чисел на компьютере, поскольку для представления значения цифры требуется всего 4 бита.

Шестнадцатеричная система (часто называемая «hex») состоит из 16 символов, поэтому в ее основе лежит число 16. В шестнадцатеричной системе используются 10 десятичных чисел и шесть дополнительных символов: A, B, C, D, E и F.

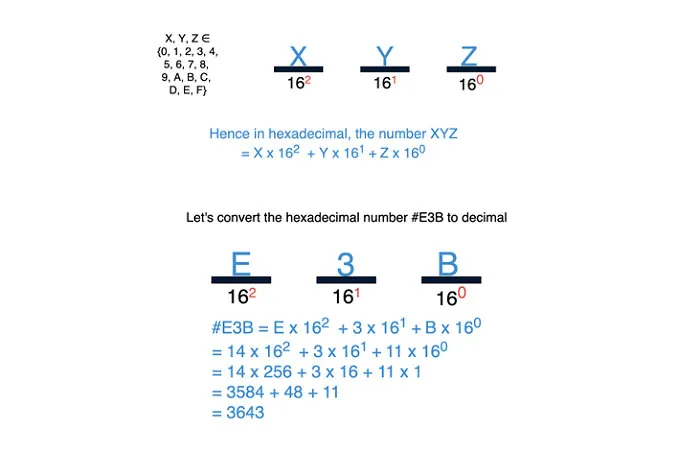
Значения цифр в шестнадцатеричной системе — это степени 16. Давайте посмотрим, что будет означать шестнадцатеричное число XYZ в десятичной системе. Как вы можете видеть ниже, шестнадцатеричным числам предшествует символ #, указывающий на то, что они имеют основание 16.

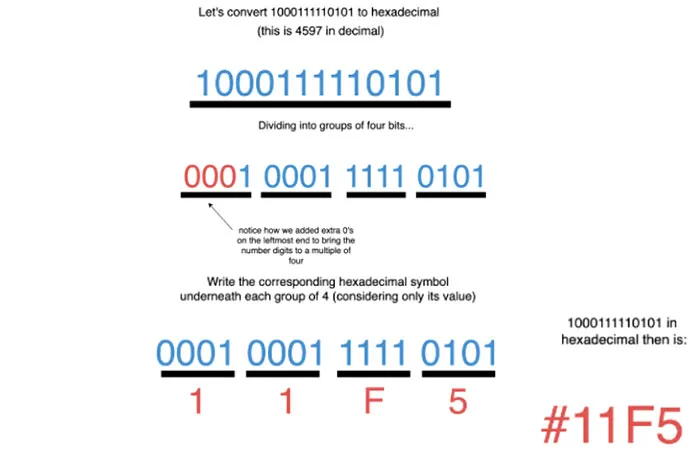
Как преобразовать двоичное в шестнадцатеричное

Теперь, когда мы знаем двоичную и шестнадцатеричную системы, давайте узнаем, как преобразовать двоичное число в шестнадцатеричное. Начнем с двоичного числа в шестнадцатеричной системе счисления.

Мы группируем двоичные цифры в квартеты (начиная сверху), а затем заменяем каждый квартет соответствующим шестнадцатеричным представлением.

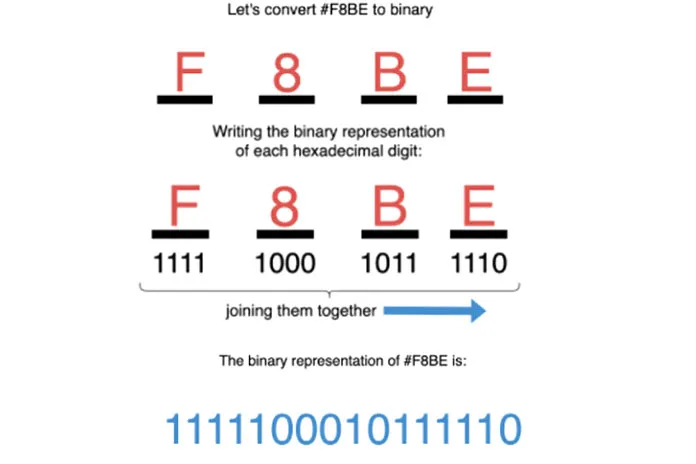
Теперь преобразуйте шестнадцатеричные числа в двоичные! Давайте рассмотрим пример. Далее каждая шестнадцатеричная цифра заменяется соответствующим двоичным квадратом.

Иногда перед значением встречается префикс 0x, указывающий на то, что следующее число следует интерпретировать как шестнадцатеричное: 0x8E — число 142 в десятичной системе счисления.

Десятичная позиционная система счисления

Индийские ученые совершили один из самых важных прорывов в математике — они изобрели систему позиционной нотации, которая сегодня используется во всем мире. Аль-Хорезми подробно описал индийскую арифметику в своей книге.

Мухаммад бин Муса аль-Хорезм

Около 850 года нашей эры он написал книгу об общих правилах решения арифметических задач с помощью уравнений. Он назывался Китаб аль-Джабр. Эта книга дала название науке алгебре.

Триста лет спустя (1120 год) книга была переведена на латынь и стала первым «индийским» учебником арифметики для всех европейских городов.

История нуля.

Нули имеют множество форм. Во-первых, ноль — это цифра, обозначающая пустое место; во-вторых, ноль — это необычное число, потому что на ноль нельзя делить, а при умножении на ноль любое число становится нулем; в-третьих, ноль нужен для вычитания и сложения, потому что иначе сколько их будет, если из 5 вычесть 5?

Нули впервые появились в древневавилонской системе счисления для обозначения недостающих цифр в числах, но такие числа, как 1 и 60, записывались одинаково, поскольку не имели нулей в конце цифр. В их системе ноль действует как пробел в тексте.

Великого греческого астронома Птолемея можно считать изобретателем нулевой формы, поскольку в его трудах вместо знака, обозначающего пространство, мы находим греческую букву омикрон, которая очень похожа на современный знак нуля. Но Птолемей использует ноль в том же смысле, что и вавилоняне. В настенной надписи в Индии девятого века нашей эры этот символ впервые встречается в конце числа. Это первое общепринятое название современного знака ноль. Именно индийские математики изобрели ноль во всех его трех значениях. Например, индийский математик Брахмагупта начал активно использовать отрицательные числа и операции с нулем уже в седьмом веке нашей эры. Но он утверждал, что число, деленное на ноль, равно нулю, что, конечно, неверно, но это настоящая математическая дерзость, которая привела к другому замечательному открытию индийских математиков. А в двенадцатом веке другой индийский математик, Башкара, предпринимает еще одну попытку понять, что происходит, когда вы делите на ноль. Он пишет: «Количество, деленное на ноль, становится дробью, знаменатель которой равен нулю. Эта дробь называется бесконечностью».

Леонардо Фибоначчи в своей работе «Liber abaci» (1202) называет точку 0 по-арабски zephirum. Слово zephirum — это арабское слово as-sifr, которое происходит от индийского слова sunya, означающего пустоту, и служит названием для нуля. Французское слово ноль и итальянское слово ноль происходят от слова zephirum. Арабское слово as-sifr, с другой стороны, дало начало русскому слову цифра, которое использовалось до середины XVII в. Латинское слово nullus (никакой) было использовано для обозначения нуля в XVI веке.

Ноль — это уникальный символ. Ноль — это чистая абстракция, одно из величайших достижений человека. Его не существует в окружающей нас природе. В ментальной арифметике можно спокойно обойтись без нуля, но не в точной записи чисел. Более того, ноль противопоставляется всем другим числам и символизирует бесконечный мир. И если «все есть число», то ничто не есть все!