Google использует префикс 0x, чтобы отличать шестнадцатеричные числа от всех остальных чисел. Чтобы перевести число 121 в восьмеричное, введите запрос 121 восьмеричное.
Системы счисления: десятичная, двоичная, восьмеричная и шестнадцатеричная. Как перевести числа из одной системы счисления в другую. Пару слов про кодирование информации
Сегодня я решил сосредоточиться на теме, которая тесно связана с программированием и информатикой — а именно на системах счисления* (особенно если мне по тем или иным причинам приходится обращаться к ней в своих сообщениях).
* Что такое система счисления в целом?
Я дам вам короткий ответ: это запись чисел по фиксированным правилам. Например, сегодня мы везде используем десятичную систему счисления и пишем число «десять» как «10» (хотя в Древнем Риме, например, использовалась своя система, и «десять» выглядело как «X»).
В принципе, каждый может придумать свою собственную систему и кодировать ею данные, если захочет (имеет ли это смысл? 🙂 ). Далее я буду упоминать только самые распространенные системы, используемые сегодня.
Основное о системах счисления
Почему я начал эту статью со слов о том, что компьютер не может «думать»? В конце концов, кажется, что он может делать много работы, он может делать многие вещи автоматически.
Дело в том, что ПК (телефон, планшет и т.д.) — это «часть оборудования», набор электронных схем, объединенных в цепь. Процессор, как многие знают, отвечает за обработку информации всего оборудования (в этом процессоре находится множество транзисторов — полупроводниковых элементов, которые могут либо «пропускать» ток, либо нет).
Поэтому компьютер «понимает» только два сигнала: либо ток есть («1»), либо его нет («0»). Отсюда же происходит двоичная система счисления. Каждое число в двоичной системе представляет собой последовательность единиц и нулей. 👇

Снимок. Число 46 в двоичной системе счисления. Пример.
Кстати, двоичную систему счисления иногда называют «машинным языком» (потому что это язык компьютеров). В таблице ниже показано, как данные хранятся на носителях информации. 👇
| Текущий | «1» | «0» |
| Поверхность магнитного диска (например, жесткого диска) | Намагниченный | Размагниченный |
| Часть поверхности компакт-диска | Отражает радиус | Не отражает луч |
Десятичная (DEC)
Нас повсюду окружают ряды цифр от 0 до 9 — одинаковые ценники в магазинах, примеры на школьных уроках и т.д. Фактически, все они являются десятичными обозначениями. Думаю, многие это знают!
Справочные данные (которые иногда необходимы):
- Латинская нотация — DEC,
- цифры, используемые для представления чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,
- Однозначные числа (примеры): 1, 5, 6; двузначные числа: 18, 78, 98; трехзначные числа: 128, 388 и т.д.
- Двузначные, трехзначные и т.д. числа называются многозначными числами,
- более подробную информацию см. в Википедии.
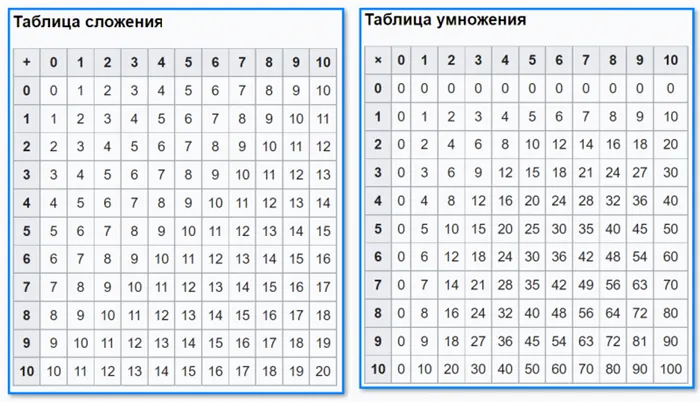
Снимок. Таблицы умножения и сложения в десятичной системе счисления.
При программировании, чтении документации и работе с HEX-редакторами мы часто используем шестнадцатеричную систему. Почему?
1. Представление целых чисел
Многие компьютерные задачи требуют обработки целочисленных данных. В основном это финансовые проблемы, где данные используются для представления инвентаря, сотрудников, запчастей, транспортных средств и т.д. Целые числа используются для представления времени и даты, а также для нумерации различных объектов: Данные таблиц, записи баз данных, адреса компьютеров и т.д. Набор целых чисел по своей природе дискретен, поскольку состоит из отдельных элементов.
Хотя любое целое число можно рассматривать как действительное число, но с дробью ноль, для целых чисел существуют специальные формы представления. Это обеспечивает эффективное использование памяти, более высокую производительность и точность вычислений за счет внедрения упорядоченного целочисленного деления.
Существует много различных способов представления целых чисел в компьютере, отличающихся количеством цифр (целые числа обычно представляются 8, 16, 32 или 64 цифрами) и наличием или отсутствием знаковой цифры.
Беззнаковое представление можно использовать только для неотрицательных целых чисел.
Чтобы получить компьютерное представление беззнакового целого числа в ячейке памяти с n цифрами, просто переведите его в двоичный формат и при необходимости расширьте результат до n цифр в левой части.
Например, десятичные числа 130 и 39 в восьмизначном представлении выглядят следующим образом:
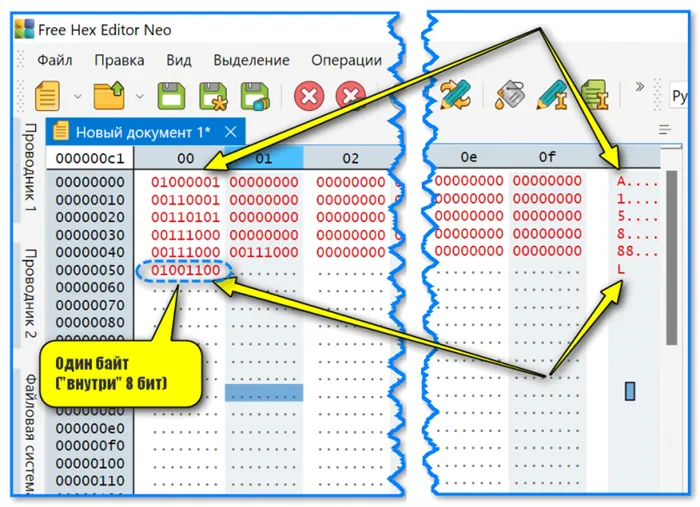
Конечно, существуют ограничения на числа, которые могут быть записаны в n-значную ячейку памяти. Максимальное значение неотрицательного целого числа достигается, когда все биты ячейки хранят единицы. Для n-значного представления оно равно 2 n-1. Минимальное число соответствует n нулям, хранящимся в n битах памяти, и равно нулю. Ниже приведены диапазоны значений для беззнаковых n-разрядных целых чисел:

В знаковом целочисленном представлении старший разряд ячейки присваивается знаку (0 для положительных чисел и 1 для отрицательных), а остальные разряды присваиваются цифрам числа.
Знаково-символьное представление числа, при котором старший разряд ячейки присваивается знаку, а остальные разряды — цифрам числа, называется прямым кодом.
Например, прямые коды чисел 48 и-52 одинаковы для восьмизначной ячейки:
Наименьшее отрицательное число, которое можно записать в знаковом представлении с n цифрами, равно 2 n-1. Максимальное положительное число, которое можно записать в знаковом представлении с n цифрами, равно 2 n-1 — 1. Ниже приведены диапазоны значений для знаковых представлений целых чисел в ячейках с разной разрядностью:

В математике множество целых чисел является бесконечным.
Компьютер работает с конечным набором целых чисел.
Прямой код положительного числа отличается от прямого кода отрицательного абсолютного числа только содержанием знакового разряда.
2. Представление вещественных чисел
В математике множество действительных чисел является непрерывным, бесконечным и беспредельным.
Попробуйте обосновать это утверждение.
Вещественные числа записываются в натуральной или экспоненциальной форме.
В жизни мы чаще всего используем натуральную форму записи чисел, где число представлено последовательностью десятичных цифр со знаком плюс или минус; знак плюс может быть опущен, а запятая используется для разделения целой и дробной частей числа.
Например: 12.34? 0.0056; -708.9.
В экспоненциальной форме действительное число a представляется как a = ± m — q p, где m — мантисса числа, q — основание системы счисления, а p — порядок числа.
Например, длина отрезка 47,8 см может быть записана следующим образом:
1) 478 — 1 0-1 см, 2) 47,8 — 10 0 см, 3) 4,78 — 10 1 см, 4) 0,478 — 10 2 см, 5) 0,000478 — 10 5 см.
Такое разнообразие способов записи одного и того же числа в экспоненциальной форме не всегда практично. Нормализованная форма используется для наглядного представления вещественных чисел на компьютере.
Нормализованное ненулевое действительное число (1) имеет вид a = ± m — q p, где p — целое число (положительное, отрицательное или нуль), m — дробь, целая часть которой содержит значащую (ненулевую) цифру, т.е. 1 ? m < q.
1) Стандарт IEEE 754.
Примеры нормализации чисел:
1) 31,415926 = 3,1415926 — 10 1 ; 2) 1000 = 1,0 — 10 3 ; 3) 0,123456789 = 1,23456789 — 1 0-1 ; 4) 0,00001078 = 1,078 — 108 -5 ; 5) 1000,00012 = 1,00000012 — 102 11 ; 6) AB,CDEF16 = A,BCDEF16 — 1016 1 .
Диапазон вещественных чисел в памяти компьютера очень велик, но все же ограничен. Набор вещественных чисел, которые могут быть представлены в компьютере, конечен.

Проиллюстрируем это на примере калькулятора, выполняющего вычисления в десятичной системе. Предположим, что на экране калькулятора десять точек:
— Гадательный знак занимает шесть позиций (одна позиция отведена под гадательный знак, четыре — под цифры гадательного знака, одна — под точку, разделяющую целую и дробную части гадательного знака); одна позиция отведена под символ «Е»; три позиции отведены под последовательность (одна — под знак последовательности, две — под цифры последовательности).
На карманных калькуляторах перед знаком указывается первая значащая цифра, с которой начинается число гадающего.
Число 12,34 будет представлено на таком калькуляторе как +1,234E+01.
Число 12,35 будет представлено как +1,235E+01.
Как известно, между числами 12,34 и 12,35 существует бесконечное количество действительных чисел, например: 12,341; 12,3412; 12,34123 и т. д.
Каждое из этих чисел представлено в нашем калькуляторе как + 1.234E+01. У нас просто не хватает цифр для последних цифр! Аналогично, когда вещественные числа представлены в компьютере, независимо от того, какие разрядные ячейки там используются.
Оказывается, что мы можем точно представить в компьютере только конечную часть множества действительных чисел, а остальные числа — только приблизительно.
Таким образом, набор вещественных чисел, представленных в компьютере, является дискретным, конечным и ограниченным.
САМОЕ ГЛАВНОЕ
В математике множество целых чисел является дискретным, бесконечным и неограниченным.
Существует несколько возможностей представления целых чисел на компьютере, которые отличаются количеством цифр (8, 16, 32 или 64) и наличием или отсутствием знакового разряда. Во всех случаях компьютерное представление целых чисел является дискретным, конечным и ограниченным.
В математике множество действительных чисел является непрерывным, бесконечным и беспредельным.
Для представления действительных чисел в компьютере используется нормализованная нотация действительного числа a = ± m — q p, где q — основание числа, p — целое число (положительное, отрицательное или ноль), m — дробь, целая часть которой содержит значащую (ненулевую) цифру, т.е. 1 ? m. < q.
Компьютерное представление вещественных чисел является дискретным, конечным и ограниченным.
В музыке информация кодируется в нотной записи (партитуре) на протяжении веков. Математические формулы используются в математике. Химические формулы используются в химии. Существует множество примеров кодирования информации.
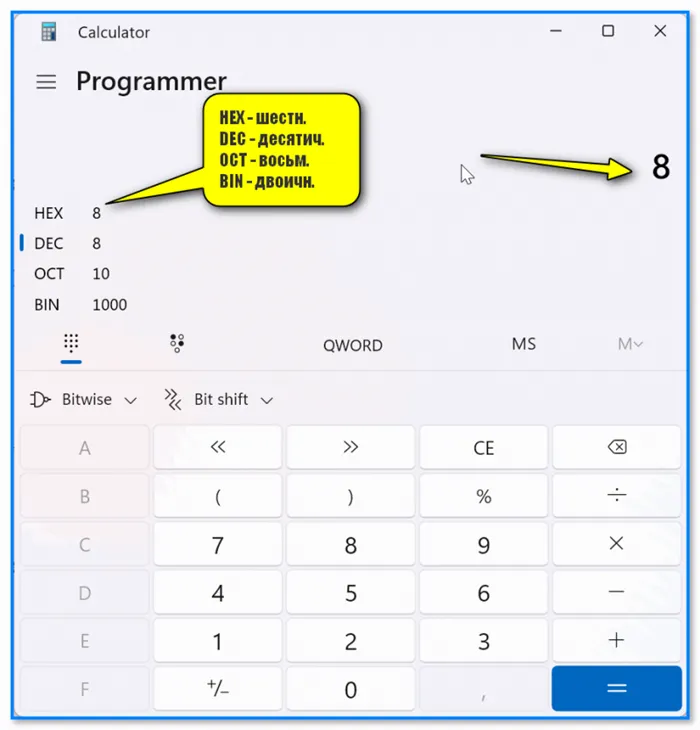
В какой системе исчисления хранит данные компьютер
Уважаемые коллеги, мы рады предложить вам разработанную нами программу обучения программированию ПЛК Beckhoff с использованием среды автоматизации TwinCAT. Курс предназначен только для самообучения и в информационных целях. Пожалуйста, свяжитесь с нами перед любым использованием предоставленных материалов в коммерческих целях. Тексты, которые копируются и публикуются в других источниках, должны содержать ссылку на сайт heaviside.ru. Вы можете обратиться к нам с любыми вопросами, в том числе о том, как настроить собственные системы мониторинга и АСУТП.
Системы нумерации
Уважаемые коллеги, эта статья посвящена теории, мы рассмотрим численные системы. Читая эту статью, вы познакомитесь с двоичной и шестнадцатеричной системами счисления. Возможно, некоторым читателям материал о системах счисления и переводе чисел из одной системы в другую покажется сложным или скучным. Тем не менее, автор настоятельно рекомендует понять хотя бы их основные принципы, поскольку они по-прежнему очень важны в программировании ПЛК, как и во многих других областях программирования, и часто требуются на практике.
Размер бита, байта и данных
В предыдущих статьях мы использовали тип данных BOOL при разработке схем на языке LD. BOOL — простейший тип данных, который может принимать только два значения: и, являются FALSE и TRUE и содержат количество информации, соответствующее биту. Бит — это наименьшее количество информации. Бит равен количеству информации, которое получается в результате одного из двух равновозможных событий. Например, подбрасывание монеты и выпадение голов или решек. Помимо битов, для представления объема информации также используется понятие байта. В современных системах принято считать, что байт состоит из восьми битов. При записи в качестве единицы измерения биты записываются как «bit», а байты — как «B», например, bit, B. Как и в других единицах измерения, перед единицей измерения используются десятичные префиксы СИ для обозначения количества информации. Кроме того, для битов и байтов используются двоичные префиксы.
| Имя | Идентификация | Степень |
| Килограмм | К | |
| мега | М | |
| гига | Г | |
| терра | Т | |
| пета | П |
Например: Kbit = Bit = KB = B.
| Имя | Идентификация | Степень | Множитель |
| Килобайт | Ki | ||
| Мегабайт | Mi | ||
| Гигибайт | Gi | ||
| тебибайт | Ti | ||
| пебибайт | Pi |
Например: Kibit = Bit = KB = B.
Когда мы пишем десятичные префиксы, мы иногда подразумеваем двоичные префиксы, т.е. когда мы пишем KB, мы подразумеваем B. Такое использование префиксов не является формально правильным, но очень часто встречается на практике.
Следует также отметить, что слово байт иногда относится к размеру регистров процессора, т.е. к количеству битов, которые процессор может обрабатывать одновременно. Размер регистров процессора называется битовой глубиной (или разрядностью) процессора. Из контекста всегда ясно, идет ли речь о бите или одном разряде процессора. Современные процессоры на базе Windows работают в разрядности или битовой глубине.
Системы нумерации
Все, наверное, знают, что компьютеры работают с данными в виде единиц и нулей. Эта система нумерации называется двоичной позиционной нумерацией. Система нумерации — это способ записи чисел. Двоичная система лучше всего подходит для использования в электронных схемах. Ноль соответствует отсутствию напряжения, единица — его наличию, или наоборот, в электронике единица часто соответствует отсутствию напряжения, ноль — его наличию.
— Гадательный знак занимает шесть позиций (одна позиция отведена под гадательный знак, четыре — под цифры гадательного знака, одна — под точку, разделяющую целую и дробную части гадательного знака); одна позиция отведена под символ «Е»; три позиции отведены под последовательность (одна — под знак последовательности, две — под цифры последовательности).
Представление чисел в компьютере. Целые числа
Оперативная память представляет собой таблицу, т.е. состоит из ячеек. Каждая ячейка памяти с произвольным доступом представляет собой физическую систему, состоящую из определенного количества однородных элементов. В ячейках оперативной памяти хранятся все данные, включая числа. Этот урок объясняет, как целые числа представлены в памяти компьютера.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим учебным видео в комплекте, вам необходимо добавить его в свой личный кабинет.
Конспект урока «Представление чисел в компьютере. Целые числа»
— Правила представления данных на компьютере,
— Набор целых чисел, представленных в памяти компьютера, является дискретным, конечным и ограниченным,
— диапазон целых чисел, хранящихся в одном байте памяти, в двух вариантах: знаковом и беззнаковом.
Скорость вычислений, объем памяти и сложность алгоритмов арифметических операций зависят от системы счисления, используемой в компьютере.
Десятичная система, к которой мы привыкли, не самая лучшая для использования в компьютерах. Надежнее и дешевле всего, если электронные компоненты, на которых основаны современные компьютеры, могут принимать только два состояния. Одно состояние может быть закодировано числом ноль, а другое — числом один. Такое кодирование называется двоичным кодированием.
Компьютеры используют двоичную нотацию, потому что она имеет преимущества перед другими системами.
— Для этого необходимо техническое устройство с двумя фиксированными состояниями.
— Представление информации только с двумя состояниями является надежным и устойчивым к шуму.
— Двоичная система счисления позволяет легко выполнять арифметические операции.
Единственным недостатком двоичной нотации является быстрое увеличение количества цифр, необходимых для хранения чисел, что может сделать нотацию более длинной.
Рабочая память компьютера состоит из ячеек, каждая из которых представляет собой физическую систему, состоящую из определенного количества однородных элементов. Эти элементы имеют два постоянных состояния, одно из которых соответствует значению 0, а другое — значению 1.

Как вы помните, данные и программы хранятся в памяти компьютера в виде 1 и 0, т.е. в двоичном виде.

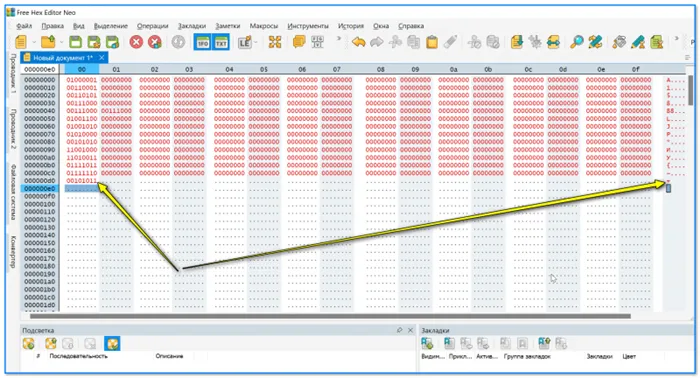
Если представить память компьютера, то она выглядит следующим образом:

Давайте объясним основные правила представления данных в компьютере.
1. данные и программы в памяти компьютера хранятся в двоичной форме.
Современные компьютеры могут обрабатывать числовую, текстовую, графическую и звуковую информацию, и этот двоичный код может относиться к любому виду данных.
2. представление данных в компьютере имеет дискретную структуру.
3. рабочая память компьютера не бесконечна, а количество величин, представленных в рабочей памяти, ограничено и конечное.

Давайте разберемся с дискретной структурой представления данных или дискретностью.
Если мы используем формат представления знаковых целых чисел, то самое большое число — 32767; если мы представляем беззнаковые целые числа, то самое большое число почти удваивается по модулю и составляет 65535.
Как переводить десятичные числа в двоичные
Эта задача напоминает математическую головоломку и может быть поставлена на школьной олимпиаде.
Чтобы научиться их решать, давайте снова рассмотрим натуральные простые числа в двоичной и десятичной системе счисления.
| Десятичное число | Двоичное число |
|---|---|
| 1 | 12 |
| 2 | 102 |
| 3 | 112 |
| 4 | 1002 |
| 5 | 1012 |
| 6 | 1102 |
| 7 | 1112 |
| 8 | 10002 |
| 9 | 10012 |
Нечетные числа 2, 4, 6 и 8 в двоичной системе счисления оканчиваются на 0. Нечетные числа 1, 3, 5, 7 и 9 оканчиваются на 1. Этому есть простое объяснение: в двоичной системе счисления 2 равно 10 в десятичной системе счисления. Когда двоичное число делится на два, оно округляется. Математики говорят, что четные числа делятся на 2 без остатка (или на 0), а нечетные — на 1:
- 4, деленное на 2, дает остаток 0,
- 5 делится на 2, остаток равен 1,
- 6 делится на 2, остаток равен 0,
- Когда 9 делится на 2, остаток равен 1.
Попробуем преобразовать десятичное число 26 в двоичное. Для этого используйте деление на 2.
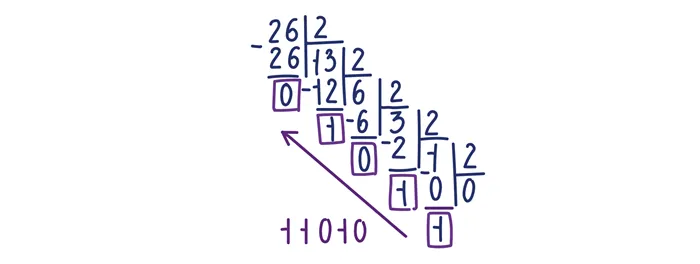
Если 26 разделить на 2, то результат будет равен 13, а остаток — 0:
- 13 делится на 2, результат — 6, а остаток — 1,
- 6 делится на 2, результат равен 3, остаток от деления равен 0,
- 3 делится на 2, результат равен 1, остаток от деления равен 1,
- 1 делится на 2, результат равен 0, остаток от деления равен 1,
Из остатков 1, 1, 1, 1, 0, 1 и 0 складываем необходимые двоичные обозначения.
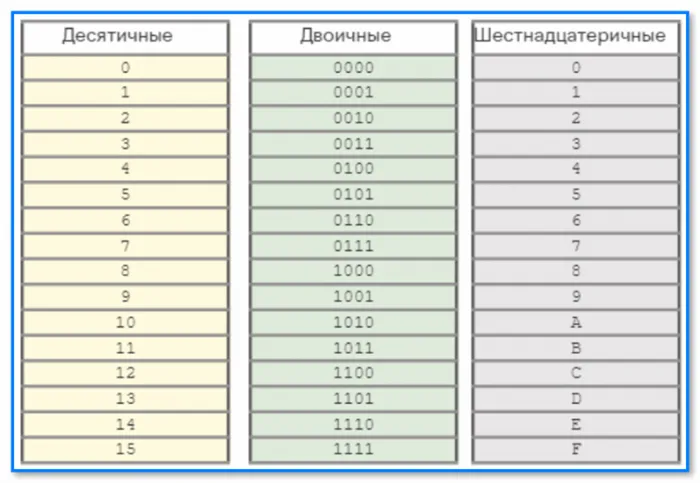
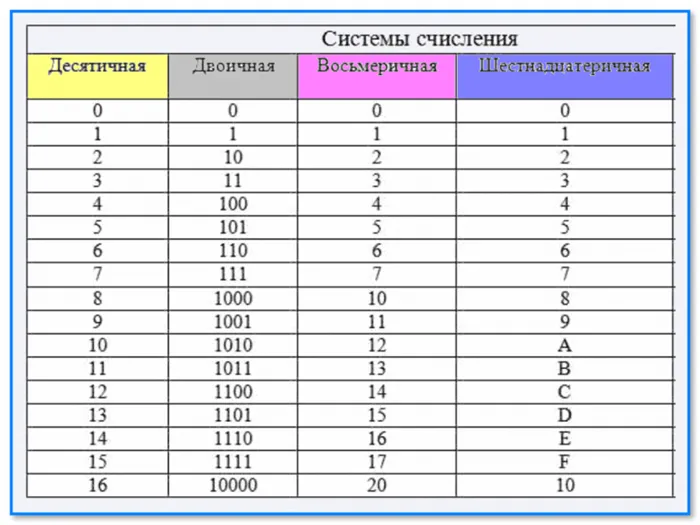
Шестнадцатеричная система счисления
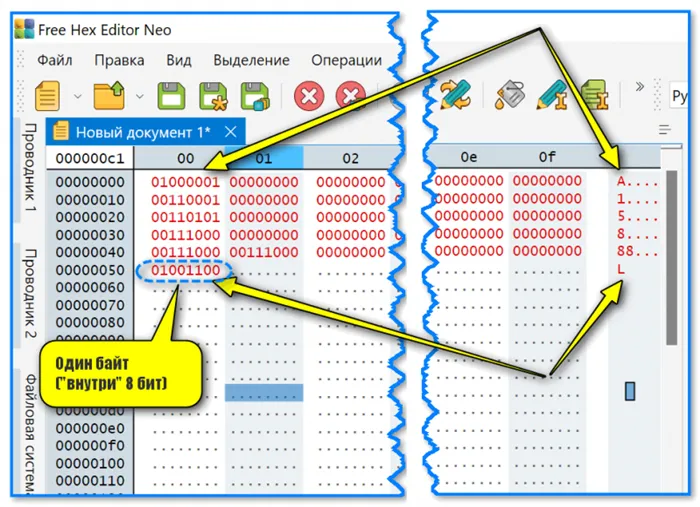
Мы знаем, что компьютер использует числа для представления разного рода информации. Например, цвета хранятся в виде трех чисел — яркости красного, зеленого и синего компонентов цвета. Каждый элемент имеет восемь двоичных цифр, связанных с ним, поэтому максимальная яркость элемента равна 111111₂ или 255. Весь цвет описывается большим 24-битным двоичным числом, например, 11111010 10000000 01110010, которое является цветом Salmon из таблицы цветов HTML.
Восемь самых высоких позиций предназначены для хранения красного компонента, восемь средних — для зеленого и восемь самых низких — для синего. Мы видим, что такая запись очень громоздка и непрактична.
Кажется более практичным записать цвет в виде десятичной дроби 16416882. Хотя он занимает меньше места, трудно понять яркость каждого элемента.
Чтобы записывать большие двоичные числа, программисты изобрели шестнадцатеричную систему счисления:
- В десятичной системе десять цифр, в шестнадцатеричной — шестнадцать.
- Десятичные числа в десять раз больше соседних, а шестнадцатиричные — в шестнадцать раз больше соседних.
Как и в двоичной системе, цифры 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 заимствованы из десятичной системы. В данном случае, однако, этих цифр недостаточно: Необходимо еще шесть. В шестнадцатеричной системе они обычно обозначаются первыми буквами английского алфавита:
| База 16 | основание 10 | База 2 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 2 | 10 |
| 3 | 3 | 11 |
| 4 | 4 | 100 |
| 5 | 5 | 101 |
| 6 | 6 | 110 |
| 7 | 7 | 111 |
| 8 | 8 | 1000 |
| 9 | 9 | 1001 |
| A | 10 | 1010 |
| B | 11 | 1011 |
| C | 12 | 1100 |
| D | 13 | 1101 |
| E | 14 | 1110 |
| F | 15 | 1111 |
Восьмеричная система счисления
Раньше восьмеричная система использовалась наравне с шестнадцатеричной. Как видно из названия, используется только восемь цифр: 0, 1, 2, 3, 4, 5, 6 и 7. Восьмеричная система подходит для представления шести-, девяти- и 12-значных двоичных чисел.
Эти цифры не являются общепринятыми. Одним из самых известных примеров восьмеричных чисел являются права доступа в операционной системе UNIX. Они записываются в виде девятизначных двоичных чисел, например, 110100100 или 111101100. Поскольку запомнить и передать эти числа сложно, программисты предпочитают восьмеричную систему и кодируют разрешения как 644 или 754.
Широко используемые операционные системы Linux и MacOS являются производными от UNIX, поэтому права доступа также задаются в восьмеричной форме.
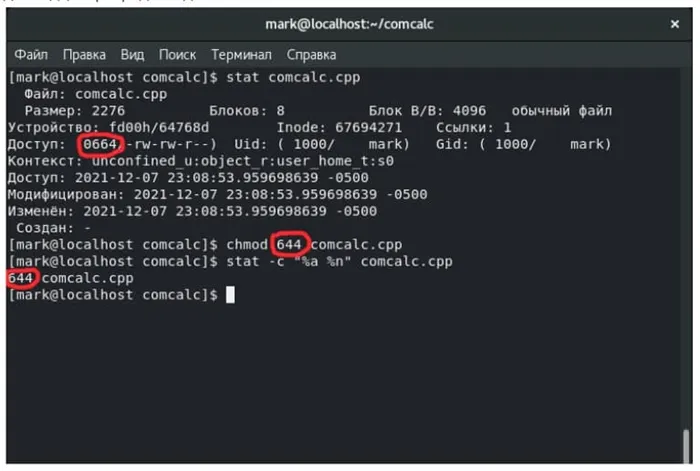
Пользователи UNIX используют команду stat для выяснения разрешений и команду chmod для их изменения. На рисунке видно, что команды stat и chmod используют восьмеричные числа. Подробное объяснение этих команд выходит за рамки данной статьи. Вы можете узнать больше о разрешениях и значении этих чисел, ознакомившись с командной строкой Linux.
В целом, восьмеричные числа в настоящее время используются редко. Подавляющее большинство программистов используют шестнадцатеричную нотацию.