Двоичное представление данных характерно для двоичного кода расположения, который составляет основу двоичной системы счисления, используемой во всех видах вычислительной техники.
1.5.1. Преобразование информации из непрерывной формы в дискретную
Для выполнения своих задач людям часто приходится преобразовывать имеющуюся информацию из одной формы представления в другую. Например, при чтении вслух информация преобразуется из дискретной (текстовой) формы в непрерывную (слуховую). В диктанте на уроках русского языка, с другой стороны, информация преобразуется из непрерывной формы (голос учителя) в дискретную (записи учеников).
Информацию в дискретной форме гораздо легче передавать, хранить или обрабатывать автоматически. Поэтому большое внимание в компьютерных технологиях уделяется методам преобразования информации из непрерывной формы в дискретную.
Дискретизация информации — это процесс преобразования информации из непрерывной формы представления в дискретную.
Рассмотрим суть процесса дискретизации информации на примере.
Метеорологические станции оснащены самопишущими приборами для непрерывной регистрации атмосферного давления. Результатом их работы являются барограммы — кривые, показывающие, как меняется давление в течение длительного периода времени. Одна из таких кривых, построенная прибором во время семичасовых наблюдений, показана на рис. 1.9.
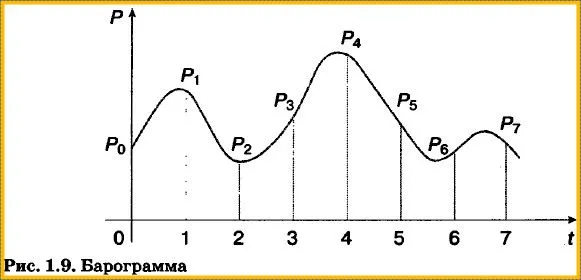
На основе полученной информации можно составить таблицу, в которой будут показаны показания в начале измерений и в конце каждого часа наблюдения (рис. 1.10).

Полученная таблица не дает полного представления о том, как менялось давление в течение периода наблюдений: например, не показано самое высокое значение давления, измеренное в четвертый час наблюдений. Однако если включить в таблицу значения давления, наблюдаемые каждые полчаса или 15 минут, то новая таблица дает более полное представление об изменениях давления.
Таким образом, информация, которая была представлена в непрерывной форме (барограмма, кривая), была преобразована в дискретную форму (таблица) с некоторой потерей точности.
Позже вы познакомитесь с возможностями дискретного представления звуковой и графической информации.
1.5.2. Двоичное кодирование
Чтобы представить информацию в дискретной форме, она, как правило, должна быть выражена с помощью символов естественного или формального языка. Таких языков тысячи. Каждый язык имеет свой алфавит.
Алфавит — это конечный набор дискретных символов, используемых для представления информации. Мощность алфавита — это количество символов, которые он содержит.
Алфавит, состоящий из двух символов, называется двоичным алфавитом (рис. 1.11). Представление информации с помощью двоичного алфавита называется двоичным кодированием. Когда мы кодируем информацию таким образом, мы получаем ее двоичный код.
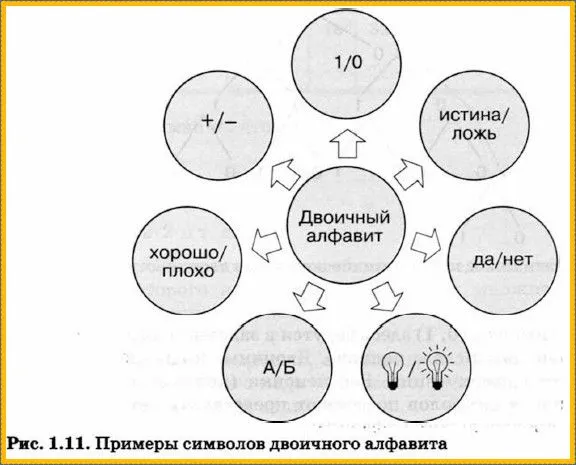
Рассмотрим цифры 0 и 1 как символы двоичного алфавита.
Покажем, что любой алфавит можно заменить двоичным алфавитом. Сначала мы присваиваем каждой букве алфавита возрастающее число. Представим число с помощью двоичного алфавита. Полученный двоичный код считается кодом исходного символа (рисунок 1.12).

Если мощность исходного алфавита больше двух, то для кодирования символа этого алфавита требуется не один, а много двоичных символов. Другими словами, цепочке (последовательности) из множества двоичных символов присваивается порядковый номер каждого символа исходного алфавита.
Правило получения двоичных кодов для символов с буквенной силой больше двух может быть проиллюстрировано схемой на рисунке 1.13.
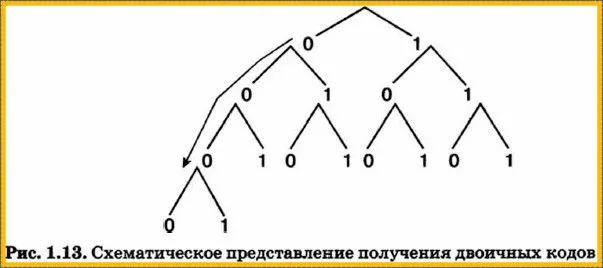
Двоичные символы (0,1) получены здесь в определенном алфавитном порядке и расположены слева направо. Двоичные коды (строки символов) считываются сверху вниз. Все цепочки (кодовые комбинации) из двух двоичных символов могут представлять четыре различных символа любого алфавита:

Строки из трех двоичных символов получаются путем умножения двузначных двоичных кодов в правой части на 0 или 1. В результате получается 8 комбинаций из трех двоичных символов, что в два раза больше, чем в случае с двумя двоичными символами:

Таким образом, четырехзначный двоичный код дает 16 кодовых комбинаций, пятизначный — 32, шестизначный — 64 и так далее.
Длина двоичной строки, т.е. количество символов в двоичном коде, называется битовой глубиной двоичного кода.

Обратите внимание на то, что:
32 = 2-2-2-2-2-2-2-2 и так далее.
Здесь число кодовых комбинаций является произведением числа одинаковых множителей, равных разрядности цифр двоичного кода.
Если обозначить число кодовых комбинаций через N, а емкость двоичных разрядов через i, то открытый закон можно сформулировать следующим образом:
В математике такие произведения записываются в виде:
N = 2 i.
Обозначение 2 i означает: «2 в i-й степени».
1.5.3. Универсальность двоичного кодирования
В начале этого раздела вы узнали, что информация, которая находится в непрерывной форме, может быть выражена символами естественного или формального языка. Символы любого алфавита, в свою очередь, могут быть преобразованы в двоичный код. Таким образом, любая информация на естественных или формальных языках может быть представлена двоичным кодом, так же как изображения и звуки (рис. 1.14). Это означает, что двоичное кодирование является универсальным.
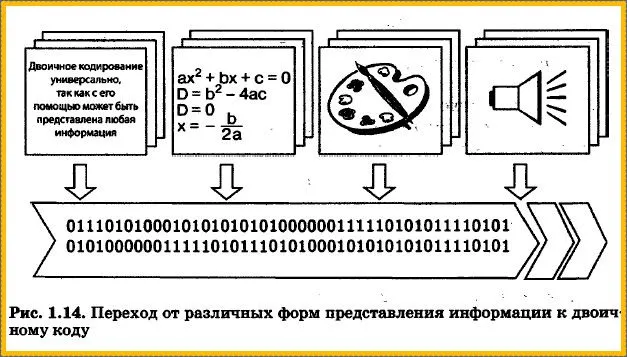
Двоичные коды широко используются в компьютерных технологиях, поскольку для их работы требуется только два состояния электронной схемы — «включено» (это соответствует цифре 1) и «выключено» (это соответствует цифре 0).
Простота технической реализации является основным преимуществом двоичного кодирования. Одним из недостатков двоичного кодирования является большая длина результирующего кода.
Однако 8-битный блок может принимать до 256 различных состояний. Эта часть двоичного кода достаточно значима, чтобы представлять один из многих вариантов.
Экскурс в прошлое
Двоичные вычисления были введены немецким математиком и ученым Вильгельмом Лейбницем в семнадцатом веке. Он считал, что двоичная нумерация проста и красива. Он сказал. Если свести числа к таким основаниям, как 0 и 1, то получится замечательный порядок».. Однако арифметика была не очень популярна. До 20-го века не было опубликовано ни одной работы по этому вопросу. Однако с появлением первых компьютеров ситуация изменилась, и мы используем их до сих пор.
Чтобы полностью понять двоичную арифметику, необходимо знать или просмотреть основные определения. Это является основой для понимания следующего текста. К ним относятся такие термины, как:
- Цифры — символы, которые мы используем для записи цифр (0-9),
- Алфавит — набор символов, которые мы используем для представления числового значения. В арабском алфавите, который используется во всем мире, символы состоят из цифр от 0 до 9.
- Цифра — это позиция (место), которую занимает цифра. Далее я покажу вам, что это такое.
- Основание — это количество символов, используемых для представления информации в нужной системе счисления. Например, в шестнадцатеричной нотации — 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F, используется 16 символов.
- Позиционные системы счисления — системы, в которых значение цифры зависит от ее положения в числе. Например, в 1000 один равен одной тысяче, а в 10 десять — десяти. Изменяется число, обозначенное цифровым символом «1».
Поняв это, мы можем перейти к сути вопроса. Итак:
Двоичная система счисления — это позиционная система, основанная на 2. Для представления чисел используются два символа — 0 и 1.
В математике он обозначается нижним индексом, на котором указано основание. Это выглядит примерно так. Натуральные числа представляются следующей формулой:
Несколько слов о том, что означают буквы в формуле:
- a — цифры (ноль или единица)
- n — номер последней цифры числа. Он начинается с 0 и отсчитывается справа налево
- k — индикатор положения
Практика
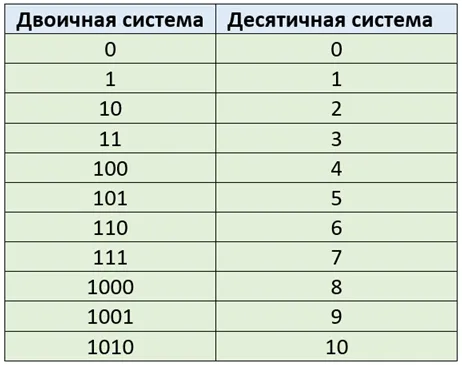
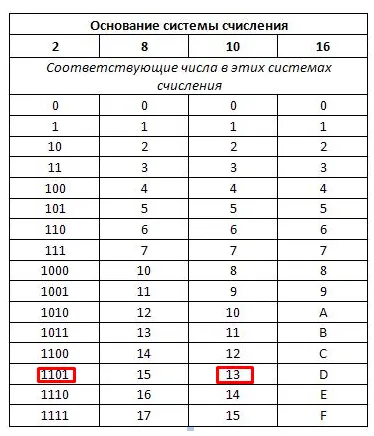
Без практики трудно объяснить, как его использовать. Итак, давайте рассмотрим несколько примеров. Но сначала нужно загрузить таблицу, в которой двоичные значения представлены в десятичной форме. Я купил первый стол, который увидел в интернете. Это выглядит примерно так:
Задание 1: Представьте число 7 в двоичной форме и запишите его по приведенной выше формуле.
Для этого нам необходимо:
Как видно из примера, здесь нет ничего сложного. Давайте сделаем что-нибудь посложнее и найдем стол побольше. Возьмите это:
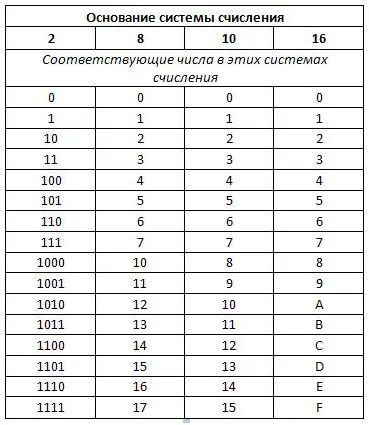
Задание 2: Рисунок 13 в двоичной системе счисления.
Шаги точно такие же, но я покажу вам другой способ выполнения первого шага. Принцип тот же, но я нахожу его более удобным.

Здесь мы берем то, что получаем
Давайте посмотрим, что находится в таблице:
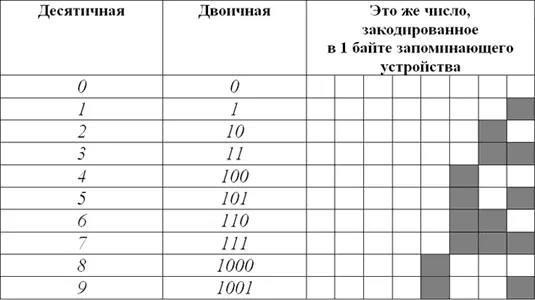
Далее я упомяну некоторые свойства, которые вы можете использовать при работе с двоичной системой.
Полезные свойства
- Добавляя ноль к правой части, вы удваиваете значение числа. Это выглядит следующим образом:
- Во всех компьютерах и других цифровых технологиях мы используем двоичные вычисления. Все дело в простоте. 0 и 1 соответствуют двум состояниям цепи — включено и выключено. Такая простая реализация обеспечивает высокую скорость и высокую помехоустойчивость всей системы.
- При шифровании сообщений. Возьмем азбуку Морзе, которая очень популярна среди радиолюбителей. Используются два сигнала: 1) длинный звуковой сигнал — тире; 2) короткий звуковой сигнал — точка.
- Каждый пиксель изображения, сохраненного в растровом формате (png, jpg, gif и другие), хранит информацию о своем цвете в трех байтах компьютерной памяти — двадцати четырех нулях и единице (двоичная нотация).
- Он является основой для «двухзначного дополнительного кода». Кодировка, используемая в компьютерах для представления отрицательных чисел. Вычитание заменяется сложением, что значительно упрощает архитектуру компьютера.
- Он является основой для работы таких устройств, как компараторы, которые преобразуют аналоговый сигнал в цифровой (широко используется в радиовещании).
Определите делитель числа. Для этого нужно переместить десятичную точку в числе вправо так, чтобы слева от нее не осталось единиц. В нашем случае мы должны переместить десятичную точку на три разряда влево. В результате мы получаем прорицателя 11001,
Двоичный код
Наиболее распространенным методом кодирования информации является двоичное кодирование. Двоичное кодирование данных используется во всех современных технологиях.
Двоичный код (бинарный код) представляет собой последовательность нулей и единиц. Это универсальная форма представления всех типов информации (текст, изображения, звук и видео). Информацию, закодированную в двоичном коде, очень легко хранить, обрабатывать и передавать с одного электронного устройства на другое, и именно в этом заключается преимущество двоичного кодирования информации.
Двоичное кодирование информации используется для самых разных данных:
- При двоичном кодировании текстовой информации буквам, цифрам и другим символам присваивается определенный код. Он хранится в памяти компьютера в виде последовательности нулей и единиц. Порядок, в котором алфавит кодируется в двоичном коде в соответствии со стандартом ASCII, является хорошим примером этого,
- Тип используемой графики влияет на способ двоичного кодирования графической информации,
- Двоичное кодирование звуковой информации осуществляется после дискретизации звуковой волны и присвоения отдельным компонентам соответствующей строки двоичных чисел,
- Двоичное кодирование видео объединяет принципы кодирования аудио и растровых изображений.
Обработка графических изображений
Текстовая, звуковая и графическая информация кодируется для обмена, обработки и качественного хранения. Кодирование информационных сообщений различных типов имеет свои особенности, но в целом приводит к их преобразованию в двоичную форму.
Рисунки, иллюстрации в книгах, диаграммы, чертежи и т.д. — являются примерами графических сообщений. Современные люди все чаще используют компьютерные технологии для работы с графическими данными.
Кодирование графической и звуковой информации — это, по сути, преобразование ее из аналоговой в цифровую форму.
Кодирование графической информации подразумевает присвоение каждому элементу изображения определенного кодового значения.
Методы кодирования графической информации уступают методам представления изображений (растровым или векторным):
- Принцип кодирования графической информации заключается в присвоении двоичного кода пикселям (точкам), составляющим изображение. Код содержит информацию о цветовом оттенке отдельных точек. Примером могут служить фотографии, сделанные цифровой камерой.
- Векторное кодирование достигается с помощью математических функций. Векторным элементам изображения (точкам, линиям и другим геометрическим фигурам) присваивается двоичная последовательность, определяющая набор параметров. Такая графика часто используется в полиграфической промышленности.
Источник
Многие могут спросить: «Какой смысл кодировать графическую информацию в виде трехмерных изображений?». Дело в том, что работа с трехмерными данными сочетает в себе методы растрового и векторного кодирования.
Кодирование и обработка графической информации в различных форматах имеет свои преимущества и недостатки.
Метод координат
Все данные могут быть переданы с помощью двоичных чисел, включая графические изображения, состоящие из серии точек. Метод координат используется для сопоставления чисел и точек в двоичном коде.
Метод координат на плоскости основан на изучении свойств точки в системе координат с горизонтальной осью Ox и вертикальной осью Oy. Точка имеет 2 координаты.
Если есть три взаимно перпендикулярные оси X, Y и Z, проходящие через начало координат, то используется метод пространственных координат. Положение точки в таком случае определяется тремя координатами.
Пространственная система координат